본 과제는 3차원 공간 상의 물체를 레이트레이싱을 활용하여 렌더링하는 프로그램을 작성하는 것이 목표로, 과제 수행을 위해선 벡터에 대한 기본적인 이해가 필수적이다.
그동안 해왔던 과제와는 결이 다른 생소한 내용이기에, 본 과제에서 필요한 개념적인 내용들을 먼저 정리해보기로 하자.
1. 벡터란?
벡터는 벡터공간 내에서 크기와 방향의 의미를 모두 포함하는 표현 도구이다.
크기와 방향을 포함하여 특정한 수치를 표현할 수 있다는 점에서 물리량을 표현하기에 적합한 도구이다.
본 과제에서는 특정한 위치에서 발사된 빛이 물체에 부딛혀 카메라까지 도달할 때, 빛의 궤적을 계산하고 그 결과를 화면 상에 뿌려주기 위해 벡터가 사용된다.

벡터를 표현하는 데 있어 중요한 것은 방향과 크기로, 그 시점과 종점은 중요하지 않다.
즉 방향과 크기가 같다면 다른 위치에 있어도 동일한 벡터로 취급된다.
2. 벡터의 크기
벡터의 크기는 시점부터 종점까지의 길이이다.
즉, 벡터의 시점과 종점을 잇는 선분의 길이가 곧 벡터의 크기이며, 해당 값은 피타고라스의 정리를 이용하여 다음과 같이 구할 수 있다.
(벡터 v의 크기는 수식 상에서 || v || 로 표기한다.)

벡터의 norm이라고 부르기도 한단다..
3. 단위벡터와 정규화
단위벡터는 벡터의 크기가 1인 벡터이다.
사칙 연산을 할 때 임의의 수 n에 어떤 수를 넣더라도 항상 n이 나오게 하는 수를 n에 대한 항등원이라고 하는데, 벡터의 항등원이 바로 단위벡터이다.
단위벡터는 크기가 1이기 때문에 특정한 스칼라 값을 곱하여 방향을 유지하면서 원하는 길이의 벡터를 생성할 수 있게 된다.
모든 벡터는 각 성분을 길이로 나눠주는 과정을 통해 단위벡터로 변환할 수 있는데, 이를 정규화라고 한다.

4. 벡터의 덧셈
두 벡터의 대응되는 성분을 각각 더해주면 벡터 간의 덧셈이 가능하다. 단, 더하고자 하는 두 벡터는 반드시 동일한 차원 상에 있어야 한다.
벡터의 덧셈에서는 교환법칙과 결합법칙이 성립한다.

벡터의 덧셈을 이용하면 한 위치에서 임의의 방향으로 임의의 거리만큼 이동한 지점을 구할 수 있다.
5. 벡터의 뺄셈
덧셈과 마찬가지로 두 벡터의 대응되는 성분끼리 빼주면 벡터 간의 뺄셈이 가능하다.
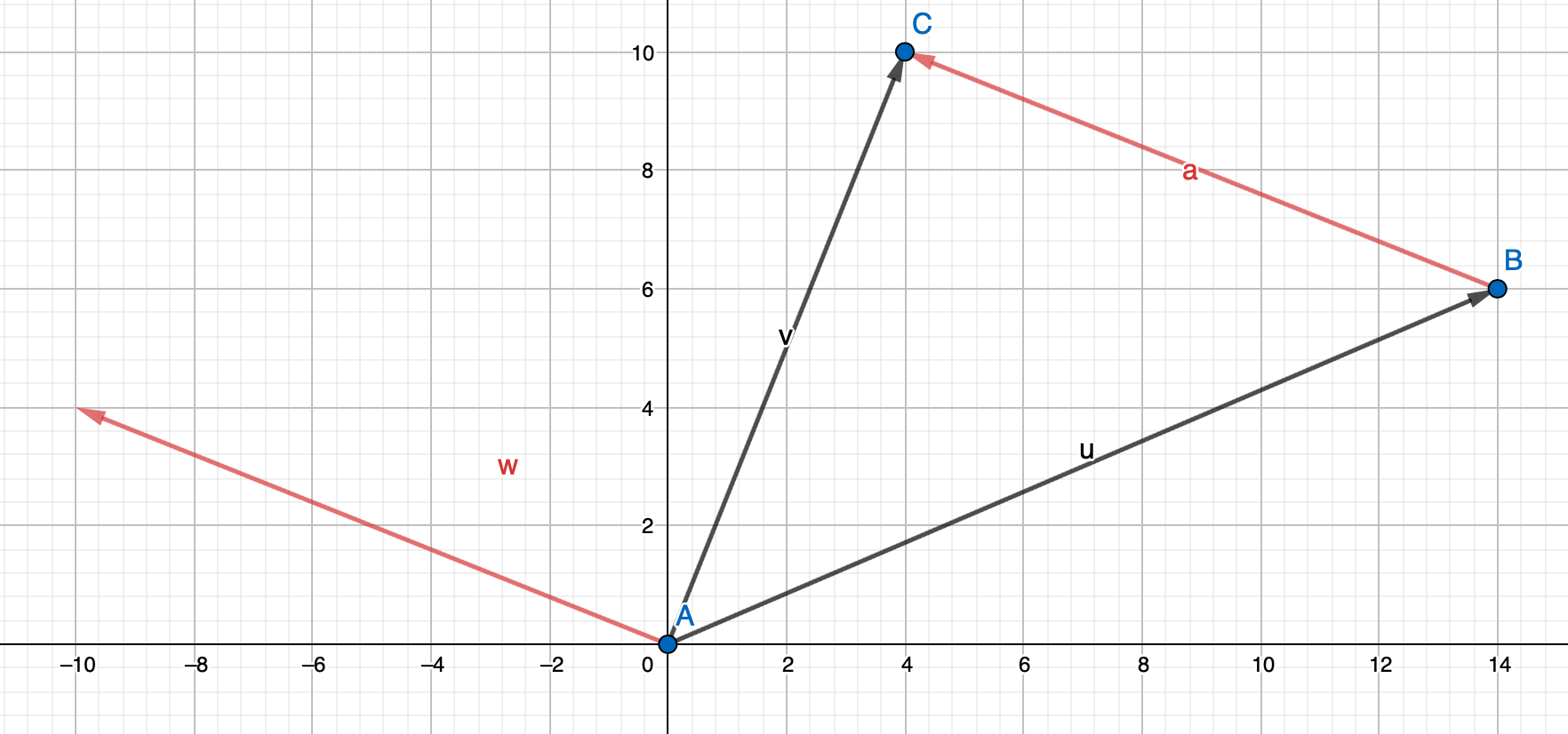
벡터의 뺄셈을 이용하면 한 위치에서 다른 위치를 바라보는 방향의 벡터를 구할 수 있다.
6. 벡터의 내적
벡터의 내적은 두 벡터의 각 성분을 곱한 후 모두 더해준 값으로 나타낼 수 있다. Dot product, 혹은 스칼라곱이라고도 불린다. 즉, 벡터의 내적 값은 벡터가 아닌 스칼라 값이다.
벡터의 내적값을 이용하여 두 벡터의 사이각을 구할 수 있다.


이때 중요한 점! 두 벡터가 단위벡터일때 서로가 직교한다면, 즉 두 벡터의 사이각이 90도라면 내적값은 0, 두 벡터가 평행하다면 내적값은 1이 나온다.
7. 벡터의 외적
벡터의 외적은 내적과는 달리 결과값이 또다른 벡터이며, 3차원 이상의 공간에서만 정의될 수 있다.

3차원 벡터의 외적은 위와 같이 계산할 수 있다. 교환법칙 성립하지 않음!!!

두 벡터의 외적으로 생성된 벡터는 각 벡터와 수직하게 된다. 즉, 이를 이용하면 한 평면의 법선벡터를 구할 수 있다.

'42 > 42cursus' 카테고리의 다른 글
| [ft_containers] 2. 템플릿 메타 프로그래밍과 is_integral, enable_if (0) | 2022.07.12 |
|---|---|
| [ft_containers] 1. Iterator 이해하기 (0) | 2022.07.08 |
| [NetPractice] 2. 라우터와 라우팅테이블 (0) | 2022.04.10 |
| [NetPractice] 1. ip와 서브넷, 서브넷 마스크 (0) | 2022.04.02 |
| [minishell] 3. 환경변수 치환 & 따옴표 풀어주기 (0) | 2022.03.28 |



댓글